Các dạng bài tập Giao thoa ánh nắng có lời giải
Với các dạng bài tập Giao thoa ánh sáng có giải mã Vật Lí lớp 12 tổng hợp các dạng bài xích tập, 100 bài bác tập trắc nghiệm có lời giải cụ thể với đầy đủ phương thức giải, lấy một ví dụ minh họa sẽ giúp đỡ học sinh ôn tập, biết cách làm dạng bài xích tập Giao thoa ánh nắng từ kia đạt điểm cao trong bài xích thi môn đồ gia dụng Lí lớp 12.
Bạn đang xem: Bài tập giao thoa ánh sáng hay và khó

Cách giải bài xích tập Giao quẹt với ánh sáng 1-1 sắc
A. Phương thức & Ví dụ
Dạng 1.1. địa điểm vân sáng, vân về tối - khoảng chừng vân
a- khoảng vân: là khoảng cách giữa 2 vân sáng gần kề
i = λD / a ( i nhờ vào λ &r
Arr; khoảng vân của các ánh sáng đối chọi sắc không giống nhau là không giống nhau với cùng một thí nghiệm).
b- địa chỉ vân sáng bậc k: Tại đó ứng cùng với Δd = d2 – d1 = k.λ , bên cạnh đó 2 sóng tia nắng truyền tới cùng pha
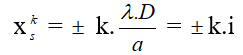
Để A là vân sáng sủa trung trọng tâm thì
k = 0 hay d = 0
k = 0: ứng với vân sáng trung tâm
k = 1: ứng với vân sáng bậc 1
…………
k = n: ứng với vân sáng bậc n.
c- địa điểm vân buổi tối thứ k + 1: Tại kia ứng cùng với Δd = (k + 0,5 ).λ . Là địa điểm hai sóng tia nắng truyền tới ngược pha nhau.
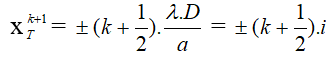
Hay vân buổi tối thứ k:

Ví dụ
Vị trí vân sáng sủa bậc 5 là:
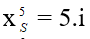
Vị trí vân buổi tối thứ 4:
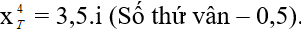
Dạng 1.2. Khoảng cách giữa những vân
Loại 1- khoảng cách vân cùng thực chất liên tiếp: l = (số vân – 1).i
Ví dụ: khoảng cách giữa 7 vân sáng liên tiếp: l = (7 – 1).i = 6i
Loại 2- giữa một vân sáng và một vân buổi tối bất kỳ:
Giả sử xét khoảng cách vân sáng sủa bậc k với vân tối thứ k’, vị trí:
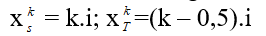
Nếu:
+ nhì vân cùng phía đối với vân trung tâm:
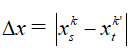
+ nhị vân khác phía so với vân trung tâm:
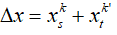
-Khoảng cách giữa vân sáng và vân buổi tối liền kề là : i/2 buộc phải vị trí vân tối những thứ liên tiếp được xác định: xt = ki / 2 (với k lẻ: 1,3,5,7,….)
VD: Tìm khoảng cách giữa vân sáng sủa bậc 5 với vân buổi tối thứ 6
Giải:
Ta bao gồm
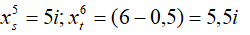
+ giả dụ hai vân cùng phía đối với vân trung tâm:
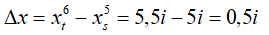
+ ví như hai vân khac phía so với vân trung chổ chính giữa :
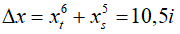
Loại 3- Xác xác định trí một điểm M bất kì trên trường giao thoa biện pháp vân trung tâm một khoảng x
M có vân sáng giỏi vân tối, bậc mấy ?
+ Lập tỉ số:

Nếu n nguyên, tốt n ∈ Z, thì tại M bao gồm vân sáng bậc k=n.
Nếu n chào bán nguyên giỏi n = k + 0,5 cùng với k Z, thì trên M có vân về tối thứ k +1
Ví dụ
Ví dụ: Một khe thon F phân phát ánh sáng đơn sắc bước sóng λ = 600nm thắp sáng hai khe song song cùng với F và cách nhau 1m. Vân giao sứt được quan gần cạnh trên một màn M song song với màn phẳng chứa F1 với F2 và cách nó 3m. Trên vị trí cách vân trung tâm 6,3m tất cả
A. Vân buổi tối thứ 4 B. Vân sáng sủa bậc 4 C. Vân tối thứ 3 D. Vân sáng bậc 3
Hướng dẫn:
Ta bắt buộc xét tỉ số x / i
Khoảng vân i= λD / a = 1,8mm, ta thấy 6,3 / 1,8 = 3,5 là một số trong những bán nguyên đề nghị tại vị trí biện pháp vân trung trọng tâm 6,3mm là một vân tối
Mặt không giống xt = (k + 0,5)i= 6,3 đề xuất ( k+ 0,5 )=3,5 phải k= 3. Vậy tại vị trí giải pháp vân trung trung khu 6,3mm là 1 vân tối thứ 4 vậy chọn đáp án A
Dạng 1.3. Khẳng định số vân bên trên trường giao thoa
- trường giao thoa xét là chiều rộng lớn của khu vực chứa toàn cục hiện tượng giao thoa hứng được trên màn- kí kiệu L.
- Số vân bên trên trường giao thoa:
+ Số vân sáng:
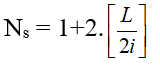
+ Số vân tối:
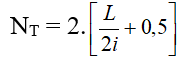
- Số vân sáng, vân về tối trong đoạn MN, cùng với 2 điểm M, N ở trong trường giao thoa nằm phía 2 bên vân sáng sủa trung tâm:
+ Số vân sáng:
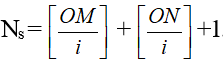
+ Số vân tối:
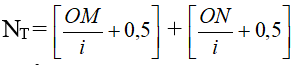
- Số vân sáng, buổi tối giữa 2 điểm MN trong khúc giao quẹt nằm thuộc phía đối với vân sáng sủa trung tâm:
+ Số vân sáng:
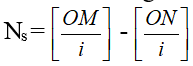
+ Số vân tối:
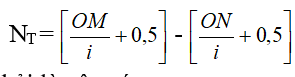
Với M, N chưa hẳn là vân sáng.
Ví dụ
Ví dụ: vào một thí điểm về Giao thoa anhs sáng bằng khe I âng cùng với ánh sáng đối chọi sắc λ = 0,7 μ m, khoảng cách giữa 2 khe s1,s2 là a = 0,35 mm, khoảng cách từ 2 khe mang đến màn quan ngay cạnh là D = 1m, chiều rộng của vùng bao gồm giao trét là 13,5 mm. Số vân sáng, vân buổi tối quan sát được bên trên màn là:
A: 7 vân sáng, 6 vân tối;B: 6 vân sáng, 7 vân tối.
C: 6 vân sáng, 6 vân tối;D: 7 vân sáng, 7 vân tối.
Hướng dẫn:
Ta có khoảng vân

Số vân sáng:
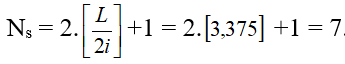
Do phân thập phân của L/2i là 0,375 T = Ns – 1 = 6 Số vạch buổi tối là 6, số gạch sáng là 7. Câu trả lời A.
Bài tập vận dụng
Trong thí nghiệm ánh sáng giao sứt với khe I âng, khoảng cách giữa 2 khe s1, s2 là 1mm, khoảng cách từ 2 khe cho màn quan gần kề là 2 mét. Hấp thụ vào 2 khe tia nắng có cách sóng λ = 0,656 m. Biết chiều rộng của ngôi trường giao sứt lag L = 2,9 cm. Xác định số vân sáng, tôi quan gần kề được bên trên màn.
A: 22 vân sáng, 23 vân tối;B: 22 vân sáng, 21 vân tối
C: 23 vân sáng, 22 vân tối
D: 23 vân sáng, 24 vân tối
Dạng 1.4. Giao trét với khe Young (Iâng) trong môi trường có tách suất là n và biến hóa khoảng cách.
Gọi λ là bước sóng ánh nắng trong chân ko hoặc ko khí.
Gọi λ" là cách sóng ánh sáng trong môi trường có tách suất n.
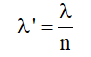
a. địa chỉ vân sáng:
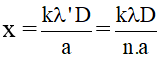
b.Vị trí vân tối:
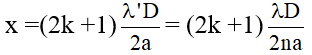
c. Khoảng chừng vân:
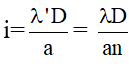
d. Khi thay đổi khoảng cách:
+ Ta có: i = λD / a &r
Arr; i tỉ lệ thành phần với D &r
Arr; khi khoảng cách là D: i = λD / a
khi khoảng cách là D’:

Nếu D = D’ – D > 0. Ta dịch màn ra xa (ứng i’ > i)
Nếu D = D’ – D 1, S2 là 75cm. Trong tương lai muốn quan tiếp giáp được vân giao thoa có khoảng vân 0,5mm thì nên phải dịch chuyển màn quan liền kề so với địa điểm đầu như thế nào?
Hướng dẫn:
Ta có

Vì ban đầu D = 75cm = 0,75m bắt buộc phải di chuyển màn quan gần kề ra xa thêm một đoạn D’- D = 0,25m.
Bài tập vận dụng
Bài tập thí nghiệm giao bôi ánh sáng solo sắc bằng khe I âng. Khi khoảng cách từ 2 khe mang đến màn là D thì điểm M bên trên màn là vân sáng sủa bậc 8. Trường hợp tịnh tiến màn xa 2 khe một quãng 80 centimet dọc con đường trung trực của 2 khe thì điểm M là vân tối thứ 6. Tính D?
Dạng 1.5. Đặt bạn dạng mỏng trước khe Young
Trong thí nghiệm giao sứt ánh sáng với khe Young (I-âng), nếu ta đặt trước khe S1 một bản thủy tinh có chiều dày e, chiết suất n.

Khi đặt bạn dạng mỏng trước khe S1 thì đường đi của tia sáng sủa S1M cùng S2M thứu tự là:
S1M = d1 + (n - 1)e
S2M = d2
Hiệu quang trình:
δ = S2M - S1M = d2 – d1 – (n – 1)e
Mà d2 – d1 = ax/D.
δ = ax/D – (n – 1)e
Vân sáng sủa trung trọng tâm ứng cùng với hiệu quang trình bởi δ = 0.
δ = axo/D – (n – 1)e = 0
Hay: xo = (n - 1)e
D / a.
Hệ thống vân di chuyển về phía S1. Vì chưng xo>0.
Ví dụ
Ví dụ: thể nghiệm giao sứt ánh sáng đối chọi sắc bằng khe I âng biết a = 0,5mm, D = 2m.. Khoảng cách giữa 6 vân sáng thường xuyên dài 1,2cm, sau này nếu sau khe S1 chắn một tấm thủy tinh phẳng mỏng manh có n = 1,5 thì vân sáng tại chính giữa bị di chuyển đến địa chỉ vân sáng bậc 20 ban đầu. Tìm kiếm bề dày e của tấm chất thủy tinh này?
Hướng dẫn:
Ta có độ di chuyển của hệ vân giao thoa = độ dịch rời của vân trung tâm.
Lúc đầu:
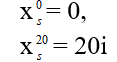
lúc sau:
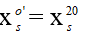
&r
Arr; Độ dịch chuyển của hệ là
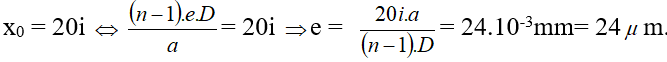
Chú ý:
+ nếu để hai bản mỏng đồng nhất trên cả hai tuyến phố truyền S1, S2 thì hệ vân ko dịch chuyển.
+ nếu để hai bạn dạng mỏng khác biệt trên cả hai tuyến đường chuyền thì độc dịch chuyển của hệ vân là |xe1 - xe2|
Bài tập vận dụng
Bài tập Trong phân tách I âng về giao thoa ánh sáng, khoảng cách 2 khe nhỏ nhắn = 0,2mm, D = 1m. Nếu đặt trước một trong các hai nguồn sáng một phiên bản mỏng bề dày e = 0,01mm, n = 1,5 bao gồm hai mặt tuy vậy song nhau thì độ dịch chuyển của hệ thống vân trên màn là bao nhiêu?
Hướng dẫn:
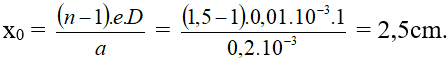
Dạng 1.6. Tịnh tiến khe sáng S đoạn y0
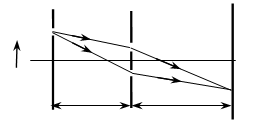
Trong xem sét Young về giao trét ánh sáng, mối cung cấp sáng S vạc ánh sáng đơn sắc có bước sóng λ. Khoảng cách từ mối cung cấp S đến mặt phẳng chứa hai khe S1; S2 là d. Khoảng cách giữa nhị khe S1; S2 là a , khoảng cách từ khía cạnh phẳng cất hai khe cho tới màn quan ngay cạnh là D.
Tịnh tiến nguồn sáng S theo phương S1 S2 về phía S1 một đoạn y thì hệ thống vân giao thoa di chuyển theo chiều ngược lại đoạn xo: xo = y
D / d
Ví dụ
Ví dụ: Trong xem sét giao thoa ánh sáng bằng khe I âng, bao gồm D = 1m, khoảng cách từ nguồn S đến 2 khe là d = 20cm. Nếu dịch rời nguồn sáng sủa S một quãng theo phương vuông góc cùng với trụ đối xứng của hệ thì hệ vân bên trên màn sẽ dịch rời như cố kỉnh nào?
Hướng dẫn:
Từ hình mẫu vẽ trên ta có: điểm O’ cùng với hiệu quang trình là:
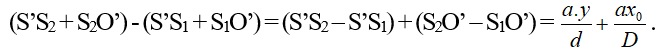
Muốn O’ là vun sáng thì
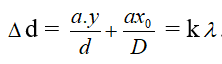
Và O’ là gạch sáng trung trung khu khi k = 0, cơ hội đó
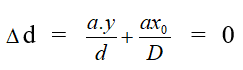
x = -Dy / d . Lốt (-) chứng tỏ vân trung chổ chính giữa sẽ dịch rời ngược chiều so với mối cung cấp sáng S một khoảng chừng
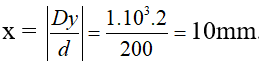
Bài tập vận dụng
Bài tập
Trong phân tách I âng về giao quẹt ánh sáng, khoảng cách giữa 2 khe sáng sủa a = 0,5 mm, khoảng cách từ khe S mang đến mặt phẳng cất 2 khe là d = 50cm. Khe S phạt ra ánh sáng solo sắc có λ =0,5 m. Chiếu sáng 2 khe hẹp. Để một vân buổi tối chiếm nơi của một vân sáng ngay tức khắc kề, ta phải di chuyển khe S theo phương S1,S2 một đoạn b = bao nhiêu?
Hướng dẫn:
Ta có độ di chuyển vân trung vai trung phong là x = b
D / d
Để mang đến vân về tối đến chiếm phần chiếm khu vực của vân sáng gần cạnh thì hệ vân phải dịch chuyển một đoạn i/2 , tức là:
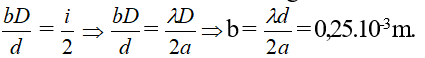
Cách giải bài xích tập Giao quẹt với ánh nắng đa sắc
A. Phương thức & Ví dụ
Nhận xét
Khi đến chùm đa sắc bao gồm nhiều bức xạ phản vào khe Y-âng để tạo nên giao thoa. Trên màn quan gần kề được hệ vân giao thoa của các bức xạ trên. Vân trung trọng tâm là sự chồng chập của các vân sáng sủa bậc k = 0 của những bức xạ này. Trên màn thu được sự ông xã chập: của các vạch sáng sủa trùng nhau, các vạch tối trùng nhau hoặc gạch sáng trùng vạch về tối giữa các bức xạ này.
Xem thêm: Dự Báo Thời Tiết Phan Thiết Hôm Nay, Dự Báo Thời Tiết Tại Thành Phố Phan Thiết
Ta có: Giao quẹt của hai giỏi nhiều bức xạ:
Dạng 2.1. Vị trí vân sáng trùng:
k1i1 = k2i2&r
Arr;...&r
Arr;k1λ1 &r
Arr; k2λ2
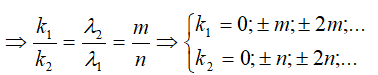
Hoặc ta hoàn toàn có thể xác định:Vị trí vân sáng của các bức xạ đối kháng sắc trùng nhau
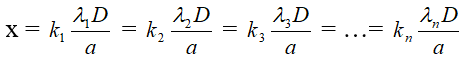
k1λ1 = k2λ2 = k3λ3 = k4λ4 = .... = knλn cùng với k1, k2, k3,…, kn ∈ Z
Dựa vào phương trình biện luận chọn các giá trị k thích hợp hợp, thường thì chọn k là bội số của số nguyên như thế nào đó.
Ví dụ:
Hai sự phản xạ λ1 và λ2 cho vân sáng trùng nhau. Ta tất cả k1λ1 = k2λ2 &r
Arr;
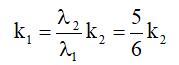
Vì k1, k2 là các số nguyên, yêu cầu ta chọn lựa được k2 là bội của 6 và k1 là bội của 5
Có thể lập bảng như sau:
| k1 | 0 | 5 | 10 | 15 | 20 | 25 | ..... |
| k2 | 0 | 6 | 12 | 18 | 24 | 30 | ..... |
| x | 0 | ..... | ..... | ..... | ..... | ..... | ..... |
Dạng 2.2. Khoảng vân trùng
(khoảng cách nhỏ nhất giữa nhị vân cùng màu với vân trung tâm):
i12 = mi1 = ni2 = ...
hoặc: i12 = BCNN(i1, i2)
Ba bức xạ: i12 = BCNN(i1, i2, i3)
Dạng 2.3. Xét ví dụ với chùm sáng gồm 2 phản xạ λ1, λ2
Loại 1: vị trí hai vân sáng trùng nhau. Bên cạnh cách bao quát trên ta rất có thể làm như sau:
+ Số gạch trùng quan gần kề được. Số vạch sáng quan tiếp giáp được:
Khi gồm giao thoa: địa điểm vân sáng:
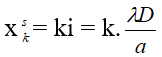
Khi 2 vân sáng sủa của 2 sự phản xạ trùng nhau:
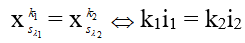

+ Số vén trùng quan sát được bên trên trường giao bôi L:
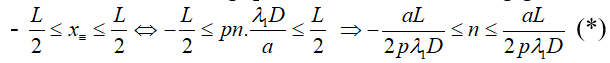
mỗi giá trị n → 1 quý hiếm k &r
Arr; số vén sáng trùng là số cực hiếm n vừa lòng (*).
+ Xét số vân trùng bên trên MN− ∈ L:
x
M ≤ x≡ ≤ x
N (x
M N; x là tọa độ) &r
Arr; khoảng chừng n &r
Arr;số giá trị n là số vân sáng sủa trùng trực thuộc + Xét số vân trùng bên trên MN−.
Chú ý: nếu M,N là vân sáng trùng &r
Arr; cần sử dụng dấu “ = „.
+ Số vun quan ngay cạnh được trên trường L:
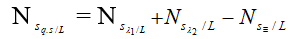
+ Số vén quan sát được trên MN− L:
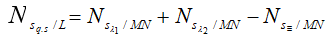
( Nhớ để ý M,N liệu có phải là vân sáng sủa trùng không )
Ví dụ
Ví dụ : Trong nghiên cứu về giao thoa tia nắng qua khe I-Âng bao gồm a= 2mm D=2m, nguồn sáng bao gồm hai sự phản xạ λ1 = 0,5μm, λ2 = 0,4μm. Tra cứu số vân sáng quan cạnh bên được trên trường giao quẹt ?
Hướng dẫn:
Ta tất cả :
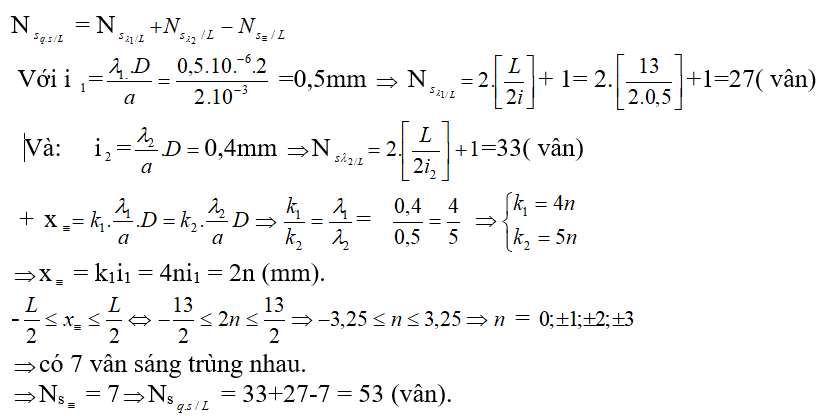
+ Bậc trùng nhau của từng phản xạ và địa điểm trung nhau:
BT trên; Tìm khoảng cách giữa 2 vân sáng sủa trùng nhau ngay gần nhau nhất?
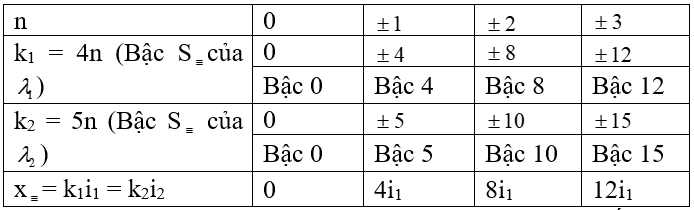
Nhận xét: khoảng cách giữa 2 vân sáng sủa trùng nhau liên tiếp là đồng nhất và là 4i1 xuất xắc 5i2.
Trong bài bác này là
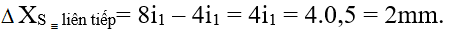
Loại 2: nhị vân về tối trùng nhau của nhị bức xạ:
- lúc vân tối của 2 phản xạ trùng nhau:
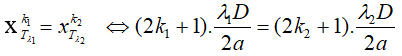

Vị trí trùng: x
x
T≡ phía bên trong vùng khảo sát:
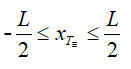
+ Số vân x
T≡ trong trường giao thoa:
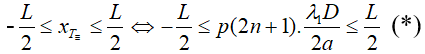
Số giá trị của n vừa lòng (∗)&r
Arr; số vân về tối trùng vào trường giao thoa.
+ Số vân x
T≡ vào miền MN−L:
x
M ≤x
T≡ ≤x
N (x
M; x
N là tọa độ và x
M N (∗∗)
Số vân buổi tối trùng vào vùng MN− là số giá trị n thỏa mãn (∗∗)
Ví dụ
Ví dụ: Trong thí điểm giao quẹt I âng triển khai đồng thời hai bức xạ 1-1 sắc với khoảng vân trên màn thu được thứu tự là: i1 = 0,5mm; i2 = 0,3mm. Biết chiều rộng trường giao sứt là 5mm, số vị trí trên trường giao thoa có 2 vân buổi tối của nhị hệ trùng nhau là bao nhiêu?
Hướng dẫn:
Khi 2 vân về tối trùng nhau:
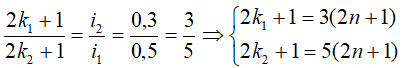
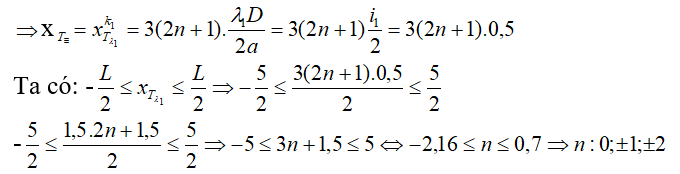
&r
Arr;có 4 vị trí vân về tối trùng nhau bên trên trường giao sứt L.
Loại 3: Vân sáng của bức xạ này trùng vân tối của bức xạ kia.
- mang sử:
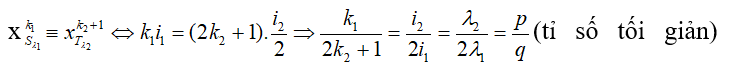
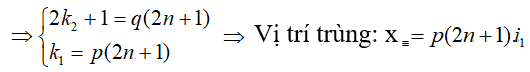
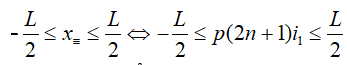
&r
Arr;số vân sáng sủa trùng vân về tối là số quý hiếm của n thỏa mãn nhu cầu biểu thức này
Chú ý: rất có thể xét x
Tλ1 = x
Tλ2
Ví dụ
Ví dụ: Trong thí nghiệm giao thoa I âng, triển khai đồng thời cùng với 2 ánh sáng solo sắc khoảng vân giao thoa trên màn theo thứ tự i1 = 0,8mm, i2 = 0,6mm. Biết ngôi trường giao thoa rộng: L = 9,6mm. Hỏi số vị trí mà :
a)x
Tλ1 = x
Sλ2 . ( -2,5 ≤ n ≤ 1,5 : tất cả 4 vị trí)
b)x
Sλ1 = x
Tλ2
Hướng dẫn:
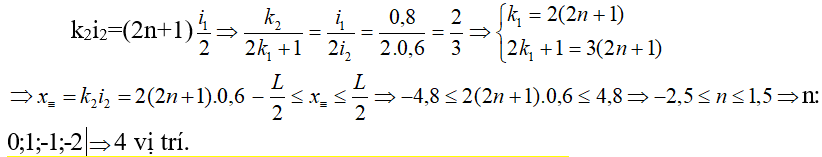
Cách giải bài tập Giao trét với ánh nắng trắng
A. Phương thức & Ví dụ

∗ thừa nhận xét: Khi tiến hành giao thoa với ánh nắng trắng ta thấy:
+ Ở ở vị trí chính giữa mỗi ánh sáng đối chọi sắc đầy đủ cho một vạch màu riêng, tổng phù hợp của chúng mang đến ta vạch sáng white (Do sự ông xã chập của các vạch màu đỏ đến tím tại vị trí này)
+ vày tím bé dại hơn λtím&r
Arr; λtím = itím.D/a nhỏ hơn và tạo cho tia tím gần vun trung tâm hơn so với tia đỏ (Xét cùng một bậc giao thoa)
+ Tập hợp các vạch từ tím cho đỏ của và một bậc (cùng quý giá k) &r
Arr; quang đãng phổ của bậc k đó, (Ví dụ: quang phổ bậc 2 là bao hàm các vén màu tự tím mang lại đỏ ứng cùng với k = 2).
Dạng 3.1. Mang lại tọa độ xo bên trên màn, hỏi trên đó gồm có bức xạ nào mang đến vạch về tối hoặc sáng?
a. Các bức xạ của ánh sáng trắng đến vân sáng tại xo khi:
Tại xo hoàn toàn có thể là quý hiếm đại số xác định hoặc là một trong những vị trí chưa khẳng định cụ thể.
Vị trí vân sáng bất kỳ x = k λD / a
Vì x = xo nên
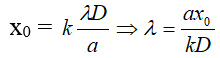
với điều kiện λ1 ≤ λ ≤ λ2,
thông thường xuyên λ1 =0,4.10-6m (tím) ≤ λ ≤ 0,75.10-6m = λ2 (đỏ)
Giải hệ bất phương trình trên,
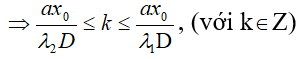
chọn k ∈ Z và thay các giá trị k tìm kiếm được vào tính λ cùng với λ = axo / k
D: đó là cách sóng các bức xạ của ánh nắng trắng mang đến vân sáng sủa tại xo.
b. Những bức xạ của ánh nắng trắng mang lại vân tối (bị tắt) tại xo:
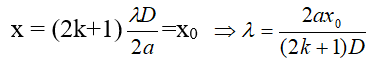
Với điều kiện:
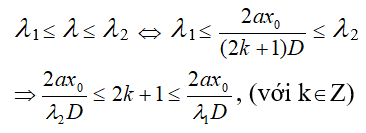
Thay những giá trị k tìm kiếm được vào :
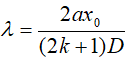
đó là cách sóng những bức xạ của ánh nắng trắng đến vân về tối (bị tắt) trên xo.
Ví dụ
Ví dụ: Trong thí nghiệm I âng về giao thoa ánh sáng, nhị khe được chiếu bằng tia nắng trắng bao gồm bước sóng từ bỏ 380nm mang đến 760nm. Khoảng chách thân 2 khe là 0,8mm, khoảng cách từ phương diện phẳng cất 2 khe mang lại màn là 2 m. Bên trên màn tại vị trí giải pháp vân trung tâm 3mm bao gồm vân sáng của các bức xạ nào?
Hướng dẫn:
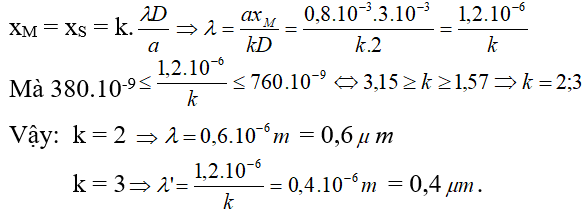
Dạng 3.2. Xác định bề rộng quang phổ bậc k trong giao sứt với ánh nắng trắng
Bề rộng quang quẻ phổ là khoảng cách giữa vân sáng red color ngoài cùng và vân sáng màu tím của một vùng quang quẻ phổ.
Δxk = xđk - xtk
Δxk = k
D(λd - λd) / a
Δxk = k(iđ - it)
với k ∈ N, k là bậc quang đãng phổ.
Ví dụ
Ví dụ: Trong thí nghiệm về giao thoa ánh sáng trắng gồm a = 3mm, D = 3m, cách sóng tự 0,4 cho 0,75 . Bên trên màn quan gần cạnh thu được những dải quang đãng phổ. Chiều rộng của dải quang đãng phổ đồ vật 2 kể từ vân sáng sủa trắng trung chổ chính giữa là bao nhiêu?
Để download tài liệu Bài tập hay và cạnh tranh phần giao trét sóng tia nắng chúng ta click vào nút tải về bên dưới.













