Thuật toán bình chọn số bao gồm phương là giữa những thuật toán khôn xiết căn phiên bản khi bắt đầu học lập trình. Nó giúp các bạn rèn luyện tính bốn duy logic. Bạn đang xem: Viết chương trình kiểm tra số chính phương


Chúng ta sẽ cùng nhau tò mò về tư tưởng số thiết yếu phương. Sau đó sẽ viết thuật toán để kiểm tra số chủ yếu phương và sau cuối sẽ là một trong những ví dụ thực nuốm được viết bằng ngôn từ C++.
Số thiết yếu phương là gì?
Theo như bọn họ đã được học ở các cấp trung học, thì số bao gồm phương được định nghĩa dễ dàng và đơn giản như sau:
Số bao gồm phương là số tự nhiên có căn bậc nhị là một vài tự nhiên, tốt nói phương pháp khác, số chính phương bằng bình phương của một số trong những tự nhiên.
Bài viết này được đăng tại
Ví dụ:
Số 4 là số thiết yếu phương vày 2^2 = 4. (hoặc sqrt(4) = 2).Tập các số chủ yếu phương như sau: CP = 4; 9; 16; 25; 26; ....Thuật toán chất vấn số bao gồm phương.
Trong phần này, mình sẽ reviews đến chúng ta hai phương pháp để viết thuật toán khám nghiệm số chính phương:
Kiểm tra số bao gồm phương bởi vòng lặp.Kiểm tra số thiết yếu phương bởi hàm sqrt() trong thư viện math.h.Thuật toán khám nghiệm số thiết yếu phương bằng vòng lặp.
Giải say đắm thuật toán:
Lặp i chạy trường đoản cú 0 đến lúc i*i > n. Trường hợp i * i = n thì n chính là số chủ yếu phương, sau đó xong xuôi chương trình.Nếu i * i > n thì n không phải là số chủ yếu phương.* lưu giữ ý: trong khoảng lặp cần có bước nhảy ++i, bởi vì vậy hãy cho bước nhảy vào trong tầm lặp, còn nếu không vòng lặp sẽ không lặp đúng như muốn muốn.
bool so
CP(int n){ int i = 0; while(i*i
Thuật toán kiểm tra số thiết yếu phương bằng hàm sqrt().
Giải mê say thuật toán:Cách triển khai này dễ dàng và đơn giản hơn không ít so với cách sử dụng vòng lặp. Trong tủ sách math.h gồm một hàm được dùng để làm tính căn bậc hai, đó chính là hàm sqrt().Chúng ta sẽ sử dụng hàm sqrt() nhằm đặt điều kiện cho số n. Ví như sqrt(n) * sqrt(n) = n, thì n đó là số thiết yếu phương cùng ngược lại.bool so
CP(int n) int sqr = sqrt(n); if(sqr*sqr == n) return true; else return false;
Ví dụ thực tế.
Trong phần ví dụ thực tiễn này, mình gồm một ví dụ như sau:Tạo mảng với số lượng phần tử do người tiêu dùng nhập.Viết hàm kiểm tra số thiết yếu phương với hiển thị tất cả các số chính phương có trong mảng.Gợi ý:
Để in ra các số bao gồm phương bao gồm trong mảng, bọn họ cần kiểm soát lần lượt các thành phần có trong mảng. Trường hợp số nào là số chủ yếu phương thì bọn họ sẽ in nó ra màn hình.Đầu tiên, họ sẽ tạo ra hàm SoCP() để bình chọn số thiết yếu phương.Tiếp đến, chúng ta sẽ tạo một mảng cất các phần tử cần soát sổ do người dùng nhập.Và cuối cùng, sử dụng vòng lặp for để lặp từng thành phần có vào mẳng. đến vòng lặp lặp từ bỏ i = 0 mang đến i
Code Mẫu:
#include #include using namespace std; bool scp(int n) int sqr = sqrt(n); return (sqr*sqr == n); int main() int n; do cout > n; while(n > a; ; cout
Kết quả:
Như vậy là họ đã thực hiện xong xuôi chương trình chất vấn số chủ yếu phương tất cả trong mảng. Cũng như chấm dứt hướng dẫn thuật toán kiểm tra số bao gồm phương. Chúc chúng ta thực hiện tại thành công!!!
Số bao gồm phương là một trong những khái niệm thú vị và hữu ích, có vận dụng rộng trong việc giải quyết các vấn đề và lập trình. Trong nội dung bài viết này, bọn họ sẽ tìm hiểu cách nhận thấy số thiết yếu phương với thuật toán chất vấn số chính phương c++ 1-1 giản, dễ nắm bắt nhất. Bước đầu thôi!
Bài trước: bài xích 14: viết công tác tính tổng theo công thức S(n) = 1+1/3+1/5+1/7…+1/(2*n-1) vào c++.
1. Số chính phương là gì?
Định nghĩa
Số chính phương giỏi square number là số bởi bình phương đúng của một số trong những nguyên.Hay hiểu đối kháng giản, số bao gồm phương là một số tự nhiên bao gồm căn bậc nhị cũng là một trong những tự nhiên. Số bao gồm phương về thực chất là bình phương của một trong những tự nhiên như thế nào đó.
Xem thêm: 34 từ vựng về các thành viên trong gia đình đầy đủ nhất, 34 từ vựng về các thành viên trong gia đình
Ví dụ, 1, 4, 9, 16, 25, với 36 là các số thiết yếu phương, do căn bậc hai của chúng (1, 2, 3, 4, 5 với 6) phần đông là các số nguyên.
Một số đặc điểm của số bao gồm phương
Các số bao gồm phương luôn là các số không âm vì chưng căn bậc nhì của một vài âm là ko xác định.Kết trái của vấn đề cộng hai số chính phương lại là một số trong những chính phương.Số chính phương ở đầu cuối của một dãy số bao gồm phương tiếp tục luôn là một vài lẻ.2. Câu hỏi kiểm tra số thiết yếu phương
Bài 15: Số chính phương hay nói một cách khác là số hình vuông, là số tự nhiên có căn bậc 2 là một số trong những nguyên. Hãy viết lịch trình nhập vào những số nguyên cho khi gặp gỡ 0 thì dừng.
Đưa ra các tác dụng sau: con số số bao gồm phương sẽ nhập (nếu không tồn tại số nào thì trả về “không tất cả số bao gồm phương làm sao được nhập”), trung bình cộng các số chính phương chẵn (nếu nó là một số trong những chẵn).
3. Thuật toán đánh giá số thiết yếu phương c++
3.1. Viết hàm soát sổ và tính tổng số thiết yếu phương
Vòng lặp do-while được sử dụng để nhập với kiểm tra những số nguyên từ tín đồ dùng cho đến khi nhập giá trị 0. Trong vòng lặp này, số n được kiểm soát xem có phải là số chủ yếu phương hay không. Nếu như n là số bao gồm phương, đổi mới dem được tạo thêm 1 và nếu n là số chẵn, tổng sum cùng soluongChan được cập nhật. Vòng lặp vẫn tiếp tục cho tới khi người tiêu dùng nhập quý hiếm 0.Sử dụng hàm tính căn bậc sqrt() trong thư viện math. Trường hợp sqrt(n)*sqrt(n) = n thì tức là n là số chính phương. Ví như như n
if (n > 0 && n == sqrt(n) * sqrt(n)) { cout
3.2 in ra số bao gồm phương trong mảng c++
Sau khi ngừng vòng lặp, lịch trình sẽ đánh giá giá trị của biến đổi dem để khẳng định có số bao gồm phương nào xuất xắc không. Nếu dem khác 0, công tác sẽ in ra số lượng số thiết yếu phương với tính trung bình cộng TBC của những số chính phương chẵn. Ví như dem bằng 0, chương trình sẽ in ra thông báo không có số bao gồm phương nào.4. Code khám nghiệm số thiết yếu phương c
#includeusing namespace std;int main() { int i, n, sum = 0, dem = 0, soluongChan = 0; float TBC; vì chưng cout > n; if (n > 0 && n == sqrt(n) * sqrt(n)) dem++; if (n % 2 == 0) sum = sum + n; soluong
Chan++; while (n != 0); if (dem != 0) { cout
5. Kết quả
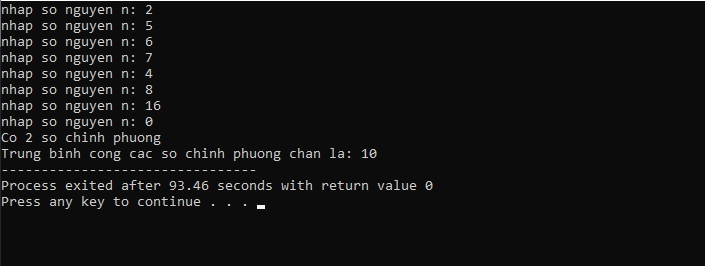
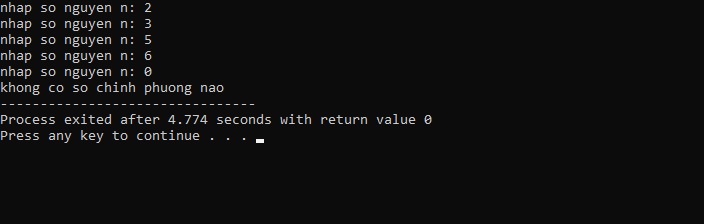
Trên đấy là một ví dụ như về việc sử dụng ngôn ngữ lập trình C++ nhằm đếm số thiết yếu phương với tính vừa đủ cộng của những số thiết yếu phương chẵn. Bằng phương pháp sử dụng vòng lặp và khám nghiệm điều kiện, chương trình cho phép người sử dụng nhập các số nguyên và xác định xem chúng có phải là số bao gồm phương hay không.
Chúng ta đã khám phá cách thực hiện hàm sqrt() để đánh giá tính chính phương của một số. Chương trình cũng đếm con số số chính phương và tính trung bình cộng của các số chủ yếu phương chẵn.
Hy vọng rằng lấy một ví dụ trên đã giúp cho bạn hiểu thêm về số thiết yếu phương với cách vận dụng nó trong ngôn ngữ lập trình C++. Cảm ơn các bạn đã theo dõi trên mailinhschool.edu.vn cùng chúc chúng ta thành công!
Tải full bài bác tập thực hành thực tế lập trình C/C++ bao gồm lời giải
Tại đây
Bài tiếp theo: bài bác 17 (TH-CSLT-01). Hãy viết lịch trình nhập vào một dãy số mang lại khi gặp gỡ số 0 thì dừng, sau đó bóc mảng c++ số chẵn với số lẻ ra 02 mảng khác nhau. Tính vừa phải cộng các số chẵn dương cùng trung bình cộng những số lẻ âm.
Câu hỏi liên quan
Các cầu là số thiết yếu phương của 180
Ước số của 180 là: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90, 180.
Các mong số thiết yếu phương của 180 là: 1, 4, 9, 36.
Vậy, các ước số thiết yếu phương của 180 là 1, 4, 9 với 36.
Số thiết yếu phương nhỏ dại nhất gồm 3 chữ số
Số chính phương nhỏ nhất có 3 chữ số là 100, bởi căn bậc hai của 100 bằng 10, với 10 là một số nguyên.
Số thiết yếu phương lớn nhất có 3 chữ số
Số chủ yếu phương lớn nhất có 3 chữ số là 961. Căn bậc nhị của 961 bằng 31, và 31 là một số trong những nguyên.
0 liệu có phải là số thiết yếu phương không
Không, 0 chưa phải là số bao gồm phương. Một vài chính phương cần là một vài nguyên dương và gồm căn bậc hai là một vài nguyên. Căn bậc hai của 0 là 0, nhưng lại 0 không thỏa mãn nhu cầu điều kiện số nguyên dương, vì chưng vậy nó ko được xem như là số chính phương.
1 tất cả phải số chính phương không
Có, một là một số thiết yếu phương. Một số trong những chính phương là một vài nguyên dương bao gồm căn bậc nhì cũng là một số nguyên. Căn bậc nhị của một là 1, và 1 là một số nguyên, bởi vì vậy nó được coi là số chủ yếu phương.













